제1장 주요내용과
질문
1.1 Set Theory
- 무한 개(countable or uncountable)의 집합에 대한 합집합과
교집합의 정의
- 분할(partition)
1.2 Probability Theory
- 확률의 공리적 정의
- [Q](Question) Borel field의 정의는 왜 필요한가?
- [Q] 왜 확률을 공리적으로 정의해야 하는가? (확률을 다르게 정의할 수 있는가?)
- 확률의 성질: [Q] 공리와 성질은 어떻게 다른가?
- Boole's inequality and Bonferroni's inequality: Theorem
1.2.11.b and equation (1.2.10)
- 중복조합(unordered-with-replacement case) 경우의 수 유도
과정을 이해하고 결과를 암기
1.3 Conditional Probability and Independence
- Example 1.3.4
- [Q] '간수가 죄수 B는 사형집행된다고 말할' 사건과 '죄수
B는 사형집행될' 사건은 같은 사건인가? 비슷한 다음 문제를 생각해 보자: 만약
김씨가 두 자녀를 두고 있다는 것을 안다고 하자. 이 때 '두 자녀 중에서 적어도 아들이 한 명 있을'
사건(사건 A)과 '김씨 집을 방문했을
때 아들 한 명을 볼' 사건(사건 B)은 서로 다른 사건이다.
사건 B가 주어지면 사건 A가 일어날 확률은 1이지만 사건 A가 주어진다고 해서
사건 B가 반드시 일어나는 것은 아니다.
- Bayes' rule
- 독립사건의 정의
1.4 Random Variables
- 확률변수의 정의
- induced probability (P와 PX
)
- [Q] 확률변수는 왜 필요한가?
1.5 Distribution Functions
- 누적분포함수의 정의와 성질
- 누적분포함수(FX) 는 확률변수의
분포(PX)를 결정한다.
(Theorem 1.5.10)
1.6 Density and Mass Functions
- 확률밀도함수의 정의와 성질
- absolute continuous function F(x)와 continuous function
F(x)의 구별
제1장 연습문제(숙제)
1 12 14 19 24 27 35 38 39
47 49 51 52 53 54 55
<12번 문제 힌트>
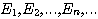 을 상호배반(pairwise disjoint)인 사건이라고 하자.
을 상호배반(pairwise disjoint)인 사건이라고 하자.
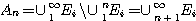 라고 정의하면,
라고 정의하면, 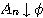 ,
, 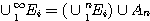 이며,
이며, 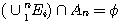 이다.
이다.
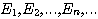 을 상호배반(pairwise disjoint)인 사건이라고 하자.
을 상호배반(pairwise disjoint)인 사건이라고 하자. 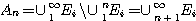 라고 정의하면,
라고 정의하면, 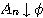 ,
, 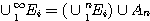 이며,
이며, 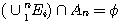 이다.
이다. 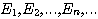 을 상호배반(pairwise disjoint)인 사건이라고 하자.
을 상호배반(pairwise disjoint)인 사건이라고 하자. 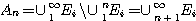 라고 정의하면,
라고 정의하면, 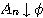 ,
, 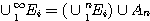 이며,
이며, 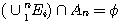 이다.
이다.