제5장 주요내용 및 질문
5.1
Basic Concepts of Random Samples
5.2
Sums of Random Variables from a Random Sample
- 통계량(statistic)과
표집분포(sampling distribution)의 정의
- [Q]
유한모집단에서 비복원 추출했을 때 표본평균의 분산은 (σ2/n)이 아니고 (σ2/n)[(N-n)/(N-1)]임을 증명하시오. 또한 E(S2)=σ2 이
아니고 σ2[N/(N-1)]
임도 증명하시오.
- convolution
formula: Theorem 5.2.9
- Example
5.2.10: For Cauchy distribution, the sample mean has the same distribution
as the individual observations. [Q] 이 사실은 정리 5.2.6에 배치되는가?
5.3 Sampling from the Normal Distribution
- 정규 확률표본(random sample from normal distribution)의 표본평균과
표본분산의 독립성 증명:
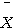 와
와 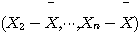 는 독립임을 이용하여 증명. (또 다른 증명: Lemma 5.3.3 (a)에 의해
는 독립임을 이용하여 증명. (또 다른 증명: Lemma 5.3.3 (a)에 의해 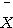 와
와 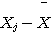 는 모든 j(=1,...,n)에 대해 독립이다. 따라서 Lemma 5.3.3 (b)에 의해
는 모든 j(=1,...,n)에 대해 독립이다. 따라서 Lemma 5.3.3 (b)에 의해 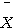 와
와 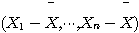 은 독립이고
은 독립이고 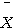 와 S2도 독립이다.)
와 S2도 독립이다.)
- [Q] (n-1)S2/σ2 가
자유도 n-1인 카이제곱 분포를 가짐을 보일 때 어려운 점은 무엇인가? [A]
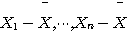 이 서로 독립이 아니라는 점.
이 서로 독립이 아니라는 점. - 카이제곱
분포의 정의와 성질: Lemma 5.3.2
- t분포의 정의와 성질; F분포의 정의와 성질; t분포와 F분포의 관계: (주의: 정리 5.3.8은 pdf를 쓰지 않고 분포의 표현적
정의(representational definition)를 이용하여 증명한다.)
5.4 Order Statistics
- 평균과 중앙값의 비교
- 이산형 분포일 때, X(j)의 cdf와 pmf: Theorem
5.4.3. 증명과정 숙지할 것
- 연속형 분포일 때, X(j)의 cdf와 pdf: Theorem
5.4.4. 증명과정 숙지할 것 (발견적(heuristic) 증명방법을
수업시간에 설명)
- 연속형 분포일 때, X(i)와 X(j)의 joint pdf: Theorem
5.4.6. 발견적(heuristic) 증명방법을 수업시간에 설명
- n개의 순서통계량(order statistics)의
joint pdf: [Q] 엄밀한 증명은 어떻게?
- 균일분포의 j번째
순서통계량(Example 5.4.5)과 범위(Example 5.4.7)의 분포는 각각 베타분포이다.
5.5
Convergence Concepts
- [Q]
표본의 크기 n이 무한히 커질 때의 통계량의 분포에 왜 관심을 갖는가?
- 거의
확실한 수렴(almost sure convergence)과 확률수렴(convergence in probability)의
구별:
[정리] almost sure convergence ⇒ convergence in probability (see
Chung(1974) for the proof)
정리의 역이 반드시 성립하지는 않음을 보이는 예(counter example)를
들어보자. (Example 5.5.8)
If a sequence of random variables converges in probability, there
is a subsequence that converges a.s. (see Chung(1974) for the proof)
- 분포수렴(convergence in distribution)의 정의: FX가 연속인 점에서만 수렴하면 된다. ([Q] 왜 이렇게 연속인 점에서만
성립하면 되는 것으로 정의하였을까?)
확률수렴(convergence
in probability)과 분포수렴(convergence in distribution)의 구별: 분포수렴은
확률변수 Xn의 수렴이
아니고 Xn의 cdf Fn의 수렴이다. 분포수렴은 확률수렴과
달리 Xn과 X의 결합분포(joint
distribution)가 필요없다.
[예]
성공확률이 1/2인 n번의 베르누이 시행에서 성공횟수를 X, 실패횟수를 Y(=n-X)라고
하면, X와 Y는 서로 다른 값을 갖는 확률변수이지만 그 분포는 같다. 이 예제는
수렴에 관한 예제는 아니지만 확률변수의 값이 같다는 것과 분포함수가 같다는
것을 구별해야 한다는 점을 보여준다.
[정리]
convergence in probability ⇒ convergence in distribution (see Chung(1974)
for the proof).
[Q] 정리의 역이 반드시 성립하지는 않음을 보이는 예(counter
example)를 들어보자.
하지만 Xn이
상수 c로 분포수렴하는
것은 확률수렴하는 것과 동등하다.
- 중심극한정리(CLT)는 분포수렴에 관한 정리이다.
정리 5.5.14는 mgf가 존재할 때의 경우인데 보다 일반적인 정리가
정리 5.5.15 이며 더 일반적인 정리 (Xi들이 같은 분포(identically distributed)를 갖는다는 가정을 할 필요없음)도
가능하다. (Lindeberg-Feller Theorem, see Chung(1974) Theorem 7.2.1)
- Slutsky's Theorem과 함께 다음 정리도 유용하게 쓰인다.
정리1: 함수 f가 연속함수이고 Xn이 X로 확률수렴(분포수렴)하면 f(Xn)이 f(X)로 확률수렴(분포수렴)한다.
위 정리의 적용 예: 표본분산 Sn2이 모분산 σ2으로 확률수렴한다면 위 정리에 의해 Sn이 σ으로 확률수렴한다.
정리2: 함수 f가 실수값을 갖는 연속함수이고 확률벡터 Xn이
확률벡터 X로 확률수렴(분포수렴)하면
확률변수 f(Xn)이 확률변수 f(X)로
확률수렴(분포수렴)한다.
위 정리의 적용 예: 확률벡터 ( Xn, Yn)이
(μ1,μ2)로 확률수렴하고 μ2≠0 이면, Xn/Yn은 μ1/μ2로 확률수렴한다. (이 예는 Slutsky
Theorem으로도 증명 가능)
- Delta method
- 확률변수 X의 분포를 알 때, 새로운 확률변수 g(X)의
근사적인 분포를 어떻게
구할 수 있는가에 대한 내용이다( Bickel and Doksum (1977), 461쪽 A.14.17 참조). 예를 들어 표본비율 p의 분산이 π(1-π)/n
일 때, logit(p)=log(p/(1-p))의 분산은 대략 얼마일까? 함수 g의 근사값으로
1차항까지의 Taylor Series 값을 이용하면, g(X)의 근사적인 분산을 구할
수 있다.
- 단변량 확률변수 X에 관한 사실을 확률벡터 X로 확장하였다 (정리 5.5.28).
- Q. 확률변수 X의 평균과 분산을 알 때 g(X)의 평균과
분산은 어떻게 알 수 있나? A. 정확한 값이 아닌 근사값(n이 클 때 정확한
값에 수렴하는 값)은 일차테일러급수(the first-order Taylor series expansion)를
이용하여 쉽게 구할 수 있다. ((5.5.8)식과 (5.5.9)식)
- Q. 확률변수 Xn이 정규분포에 수렴한다면 g(Xn)의 분포는? A. 델타방법에 의하면 g(Xn)의 분포도 정규분포에 수렴함을 보일 수 있다. 델타방법은 중심극한정리를
확장시킨 것으로 볼 수 있으며, 일차테일러급수(the first-order Taylor
series expansion)와 Slutsky 정리로부터 유도된다 (정리 5.5.24와 증명)
- 이차델타방법(second-order Delta method, 정리 5.5.26)과 다변량델타방법(multivariate
delta method, 정리 5.5.28)
- 오즈(odds)와 오즈비(odds ratio)의 의미; 추정오즈의 분산 구하기:
예5.5.19, 예5.5.22.
5.6 Generating a Random Sample
- 균일분포 난수 (uniform random number)를 이용하여 원하는 분포를
갖는 난수를 생성하는 방법을 직접적인 방법(direct methods)와 간접적인 방법(indirect
methods)로 나누어 설명.
- 직접적인 방법: 확률적분변환(probability integral transform)에
의해 지수분포 난수를 생성할 수 있고, 따라서 짝수 자유도를 갖는 카이제곱분포,
감마분포, 베타분포 난수를 생성할 수 있다 - (5.6.5).
- 닫힌 형식(closed-form)의 F-1(u)를 구할 수 없을 때: 예 5.6.4 또는 간접적인 방법을 이용
- 이산형 분포의 난수 생성 방법: (5.6.7), 예 5.6.5, 예 5.6.6.
Q. 다항분포(multinomial distribution)를 갖는 난수를 어떻게
생성할 수 있나?
- 간접적인 방법
Accept/Reject Algorithm: 예 5.6.7로 아이디어 설명. 정리 5.6.8과
예 5.6.9. (예 5.6.7은 V의 분포가 균일분포 U(0,1)인 특수한 경우로
볼 수 있음)
정리 5.6.8로부터, 원하는 분포의 난수 하나를 생성하기 위해
필요한 시행횟수의 기대값이 M임을 알 수 있음 (정리 5.6.8 다음 문단에
있는 내용 참조)
Metropolis algorithm: 정리 5.6.8에서 유한한 M값을 갖는 candidate
density fV를 찾을 수 없을 때 적용할 수 있는 방법. 증명은 생략. 난수의 수열
Z1, Z2, ...이 생성되며 초기에
생성된 난수는 쓸 수 없음. 얼마나 많은 난수를 버려야 하는지를 알 수 있는
방법이 필요.
제5장 연습문제(숙제)
1 2 6 10 13 14 17 18
29 30
31 32 35 43 44 47 48 49
50 56 60 (There are typos in Exercise 5.44, and 5.60)
Typo in 5.44: In (c), 2n should be 4n
Typo in 5.60: P(W<w) should be P(X<w, Y<f(X))
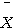 와
와 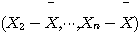 는 독립임을 이용하여 증명. (또 다른 증명: Lemma 5.3.3 (a)에 의해
는 독립임을 이용하여 증명. (또 다른 증명: Lemma 5.3.3 (a)에 의해 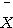 와
와 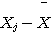 는 모든 j(=1,...,n)에 대해 독립이다. 따라서 Lemma 5.3.3 (b)에 의해
는 모든 j(=1,...,n)에 대해 독립이다. 따라서 Lemma 5.3.3 (b)에 의해 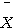 와
와 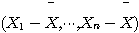 은 독립이고
은 독립이고 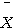 와 S2도 독립이다.)
와 S2도 독립이다.)
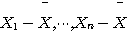 이 서로 독립이 아니라는 점.
이 서로 독립이 아니라는 점.